「深度学习基础」余弦退火学习率-PyTorch版
模型训练Trick
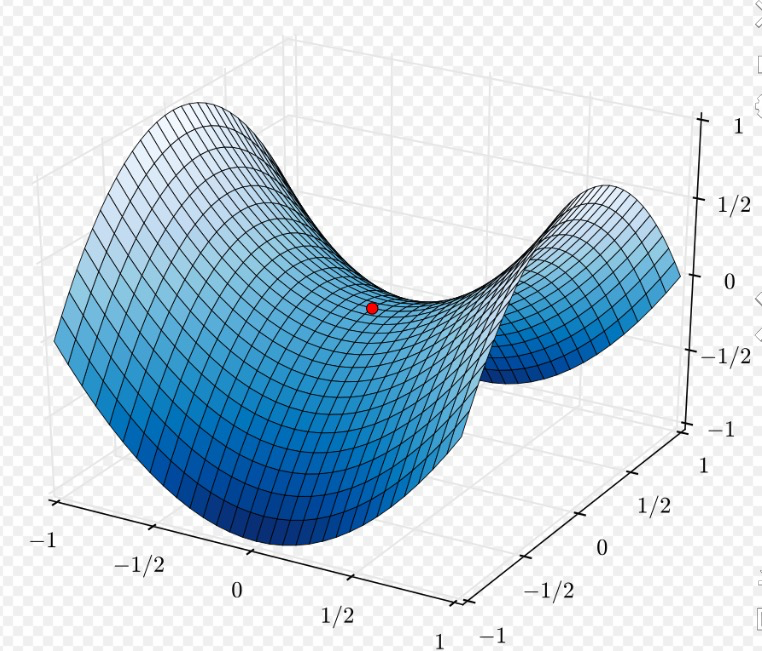
背景:深层神经网络难训练是因为学习过程容易陷入到马鞍面中,即在坡面上,一部分点是上升的,一部分点是下降的,如图在z轴上是最小值,而在x轴上是最大值。马鞍面上损失对参数的一阶导数为0,二阶导数的正负值不相同,由于梯度为0,模型无法进一步更新参数,因此模型训练容易陷入马鞍面中不再更新。
而余弦退火学习率可以很好的改善这个问题,这个是Pytorch官方的介绍。
但是官方的介绍里只有公式,没有告诉我们如何使用。
公式看不懂的同学不用担心,PyTorch都给我们封装好了,使用起来非常简单,PyTorch自带两个余弦学习率调整的方法,一个是CosineAnnealingLR,另一个是CosineAnnealingWarmRestarts。
CosineAnnealingLR
1 | CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1, verbose=False): |
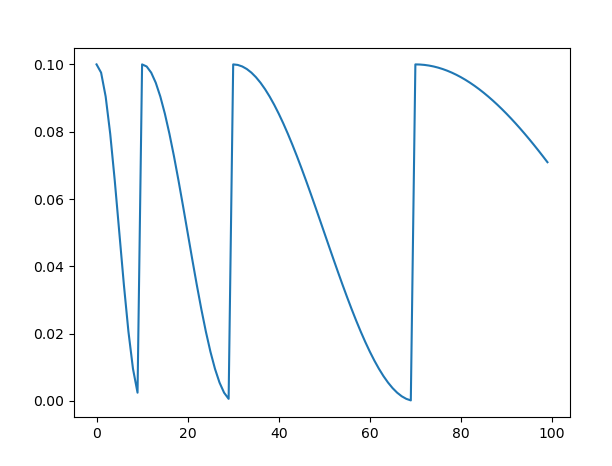
这个比较简单,只对其中的最关键的Tmax参数作一个说明,这个可以理解为余弦函数的半周期.如果max_epoch=50次,那么设置T_max=5则会让学习率余弦周期性变化5次。学习率图像大概长成这样:

CosineAnnealings
1 | CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1, verbose=False): |
这个是带热重启的学习率,这个最主要的参数有两个:
-
T_0:学习率第一次回到初始值的epoch位置
-
T_mult:这个控制了学习率变化的速度
-
-
如果T_mult=1,则学习率在T_0,2T_0,3T_0,…,i*T_0,…处回到最大值(初始学习率)
-
- 5,10,15,20,25,…处回到最大值
-
如果T_mult>1,则学习率在T_0,(1+T_mult)*T_0,(1+T_mult+T_mult2)*T_0,…,(1+T_mult+T_mult2+…+T_0**i)*T0,处回到最大值
-
- 5,15,35,75,155,…处回到最大值
-
这个的图像大概长成下边这样,根据设定的参数不同具体数值会有所区别。
所以可以看到,在调节参数的时候,一定要根据自己总的epoch合理的设置参数,不然很可能达不到预期的效果,经过我自己的试验发现,如果是用那种等间隔的退火策略(CosineAnnealingLR和T*mult=1的CosineAnnealingWarmRestarts),验证准确率总是会在学习率的最低点达到一个很好的效果,而随着学习率回升,验证精度会有所下降.所以为了能最终得到一个更好的收敛点,设置T_mult>1是很有必要的,这样到了训练后期,学习率不会再有一个回升的过程,而且一直下降直到训练结束。
示例代码
余弦学习率使用起来非常简单,只需要在每一个epoch的training和validation之后加上scheduler.step()就可以完成学习率的调整
1 | import torch.optim.lr_scheduler as lr_scheduler |
总结
余弦学习率理解起来非常简单,用起来也是很方便。
用李宏毅老师的话,这都是古圣先贤的意思,用就对了。大杀器啊,以后训练模型可能都会选择用一下。
我的理解是使用余弦退火的时候可以很直观的看到哪些学习率是比较合适的,这对我们选择正确的学习率参数很有帮助,可以逃离局部最优值。